粒子の集団運動を数学で描く（運動論的方程式）

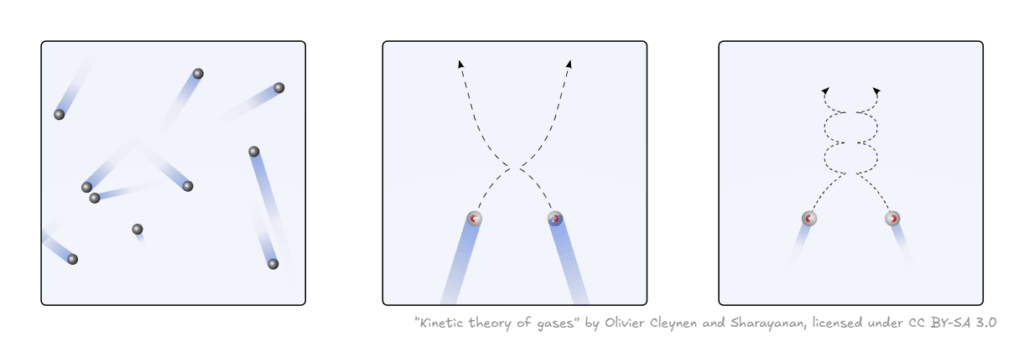
空気は、たくさんの粒子が集まってできている気体です。粒子は自由に動き回り、互いにぶつかり合いながら、全体として流れのように振舞います（ボルツマン方程式）。オーロラや太陽から吹く風（太陽風）は、電荷を帯びた粒子が集まってできている「プラズマ」と呼ばれる気体です。プラズマの中では電子やイオンが電場・磁場の中で動き回り、互いにぶつかり合いながら、自由に加速したり、波のようにそろって動いたりします（ヴラソフ–マクスウェル方程式）。

こうした粒子の集団運動は、特に、希薄な場合には、温度や圧力といった平均的な量で状態を表すことが困難になります。そこで、粒子ひとつの速さやぶつかる確率に注目することで、その集団の振舞いを数学的に厳密に記述することが可能となります。

粒子運動の確率的記述について数理的な構造や性質を明らかにし、その仕組みを理解することに関心を持っています。

ミクロからマクロへ（流体力学極限）

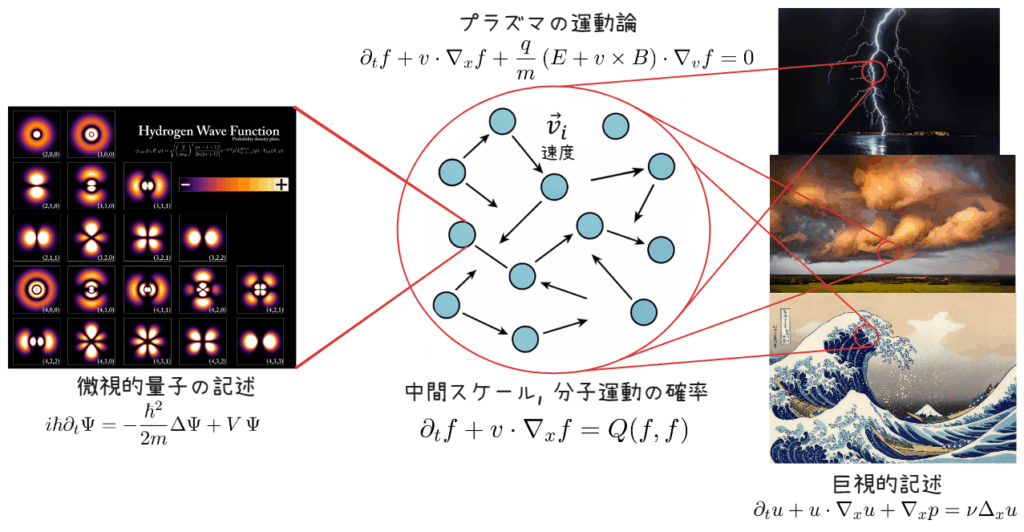
自然界の現象はどの大きさで観察するかによって、全く異なる姿を見せます。例えば、電子のような極小の世界では、状態を確率で表現する「量子力学」の法則が働きます。また、多くの分子がぶつかり合う中間の世界では、「ボルツマン方程式」による集団運動の確率的な運動論によって記述されます。さらに、雲や波のようにたくさんの粒子が集まってできる流れの大きな世界では「流体方程式」によって、流れの運動を表すことができます。そして、光速に近い粒子や宇宙ジェットの流れの世界では、「相対論的運動論や流体力学」によって、その運動を理解できます。

これらの方程式は、別々の世界の法則のように見えますが、実はつながっています。物理学を公理化することで、ミクロな法則からマクロな法則がどのように生まれるのか、その数理的な橋渡しを明らかにすることに興味を持っています。

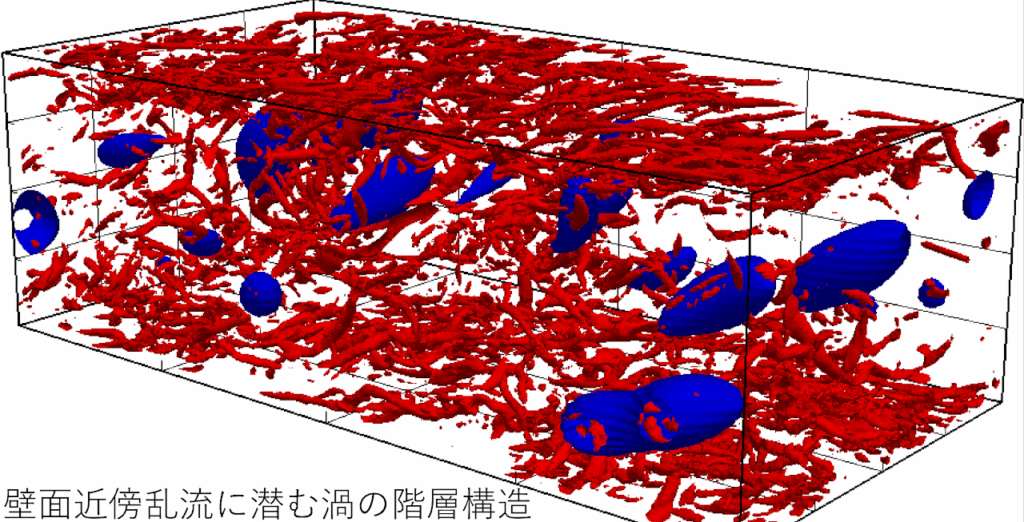
乱流の動力学

我々の身の回りにある水や空気の流れは乱流と呼ばれる不規則で複雑な運動をしています。乱流には、例えばコーヒーにミルクを早く溶かすという、混合を促進する喜ばしい効果と、投げたボールの球速が落ちるという、抵抗が増加する避けたい効果が存在します。工学的社会的な疑問にとどまらず、乱流は大きな自由度を持つカオス現象の典型例として、数学・物理学的な興味を集めてきました。この意味で乱流は多くの分野を横断する研究対象です。一見、複雑に見える流れの中に、自己相似的な秩序運動を見つけることができます。この秩序運動は乱流が自発的に振舞うのですが、その理由は、理論的に明らかになっていません。大規模数値計算とカオス力学系理論を用いた理解と応用に興味持っています。

keywords：カオス，大規模数値計算，基礎工学

地球惑星規模の流体現象

惑星大気にはジェット流と呼ばれる東西方向の強い流れが存在します。例えば、木星には約20本、金星には1本、地球には5本のジェット流が観測されています。惑星の自転によるRossby波がジェット流の形成に寄与していると考えられますが、その詳細はわかっていません。惑星規模の流体現象における波動と乱流による渦運動の相互作用に興味を持ち、ジェット流(帯状流)に関する基礎研究を行っています。

keywords：波動乱流，安定性，応用数学